Parabéns a todos que se desafiaram a solucionar o Giant Puzzle #6! Admiramos imensamente aqueles que se arriscam a pensar fora da caixa e a encontrar soluções criativas para problemas complexos.
Conseguiram resolver esse puzzle:
- Leonardo Joau
- Gabriel Tostes
- Caio Costa
- Hector Lise de Moura
- Samir Rodrigues Vieira
- Olavo Longo
- Edson Bersan
- Igor Magalhães
- Paulo Diniz
- Gilmar Santos Jr
- Ellison Cardoso
O problema
Suponha que uma formiga esteja fazendo um passeio aleatório por um cubo situado no octante positivo. A probabilidade de ela partir de um vértice e chegar a qualquer outro vértice é inversamente proporcional à distância euclidiana entre eles. Ela parte da origem do sistema (0, 0, 0) e deseja chegar no vértice situado no extremo oposto, (1, 1, 1). Note que ela pode ir do vértice (0, 0, 0) ao (1, 1, 1) em apenas um passo.
a) Qual o valor esperado de passos para a formiga chegar ao vértice oposto?
b) Qual o valor esperado de passos para a formiga chegar ao vértice oposto, dado que o último vértice que a formiga atingiu antes de chegar ao extremo oposto é (1, 1, 0)?
c) Suponha que a formiga esteja fazendo agora um passeio aleatório por um hipercubo de dimensão 7, partindo da origem (0, 0, 0, 0, 0, 0, 0) e que seu objetivo seja chegar a (1, 1, 1, 1, 1, 1, 1).
c.1) Qual seria o valor esperado de passos para chegar a tal vértice?
c.2) E se o vértice anterior ao último for (1, 1, 1, 1, 1, 1, 0)?
Observação: Forneça as respostas com pelo menos 6 casas de precisão.
Solução
Para resolver o problema, seja u um determinado vértice do cubo e Vu o conjunto dos vértices vizinhos a u. Se f(u) é o valor esperado de passos para se chegar ao vértice final partindo-se de u e p{u, v} é a probabilidade de a formiga ir de u a v, temos que:
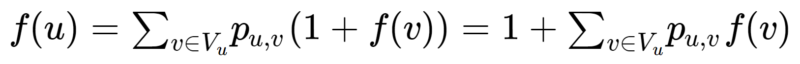
Assim, precisamos resolver um sistema linear da forma Ax = b para chegarmos à solução, onde os coeficientes da matriz A são iguais a 1 na diagonal principal e a -p{i,j} na linha i e coluna j (i ≠ j). Já os coeficientes de b são todos iguais a 1, exceto pelo último, que é correspondente ao vértice final (e, portanto, igual a 0).
Já para o problema em que a penúltima casa está pré-determinada, precisamos transformar as probabilidades utilizadas acima em probabilidades condicionais. Se x é o penúltimo vértice, devemos utilizar no sistema acima p{u , v|x}, que é a probabilidade de se ir de u para v dado que x é o penúltimo vértice e que se está no vértice u. Essa probabilidade é igual a:
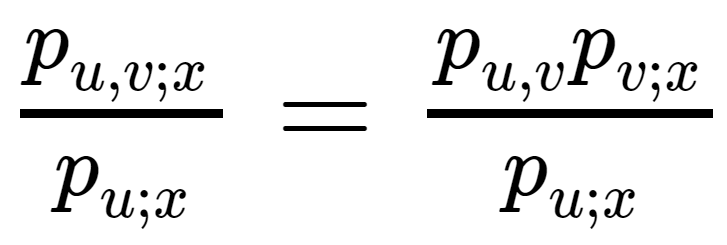
, onde p{v;x} é a probabilidade de x ser o penúltimo vértice partindo-se de v.
Chamando-se p{u;x} de g(u) e de y o vértice final, temos o seguinte sistema de equações válido para todos os vértices diferentes de x:
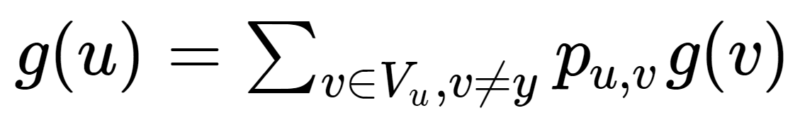
Já para x, temos:
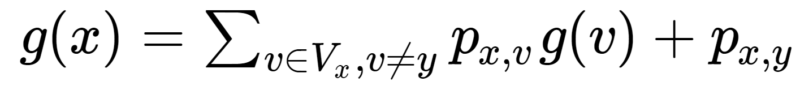
Ou seja, estamos considerando a possibilidade de a formiga andar para y apenas quando ela vem do vértice x. Neste caso, os coeficientes da matriz A serão 1 na diagonal principal e -p{i,j} na linha i e coluna j (i ≠ j), enquanto da matriz b será igual a p{x,y} na linha x e 0 nas demais linhas.
Substituímos os valores encontrados para obtermos as probabilidades condicionais e resolvemos novamente o sistema do caso sem probabilidades condicionais, apenas alterando-se os valores de tais probabilidades.
Portanto,
a) 7.307727264612062
b) 8.022339739437472
c.1) 127.43899470066293
c.2) 128.36132168842823
O código da resolução está disponível para consulta através do link: https://github.com/giant-steps/giant-puzzle-6

