As limitações do modelo de alocação de Markowitz
O modelo de alocação de Markowitz (1952), embora reconhecido como um importante avanço teórico e marco inicial na moderna teoria financeira, apresenta dificuldades conceituais e de implementação que impediram sua plena adoção entre praticantes. Uma das principais dificuldades é na estimação dos parâmetros do modelo (uma carteira com n ativos exige a estimação de n retornos e uma matriz n x n de covariâncias). O procedimento usual é estimar os parâmetros a partir da série histórica de retornos dos ativos. Esse procedimento produz resultados insatisfatórios conquanto os parâmetros sejam instáveis no tempo – como é geralmente o caso para os retornos, parâmetro crítico para a otimização de carteira. Outra dificuldade do modelo é que frequentemente produz alocações extremas, concentradas em alguns poucos ativos e “zerado” nos demais. Adicionalmente, a alocação ótima pode mudar drasticamente de um período para o outro – o que é difícil de implementar na prática, principalmente para grandes carteiras. É possível atenuar essas dificuldades impondo-se restrições, por exemplo exposição mínima e máxima por ativo e restrições de turnover. Porém essas restrições são arbitrárias e, frequentemente, refletem os vieses do investidor – justamente os vieses que se deseja evitar através da alocação sistemática.
O modelo proposto por Fischer Black e Robert Litterman
Fischer Black e Robert Litterman (B-L) propuseram um novo modelo em 1992 utilizando o mesmo arcabouço de média-variança introduzido pioneiramente por Markowitz, mas buscando superar algumas das dificuldades inerentes àquele modelo. O modelo de B-L parte da chamada “carteira de mercado de equilíbrio” – a carteira que, no contexto de CAPM, representa a alocação agregada do universo de investidores. O insight de B-L foi usar o modelo Markowitz de forma reversa para inferir retornos e covariâncias implícitos na carteira de mercado. Em seguida, B-L faz uso engenhoso do Teorema de Bayes para obter parâmetros que combinem as expectativas do investidor com aquelas inferidos da carteira de mercado, chegando a uma expectativa posterior híbrida. Por fim, utiliza otimização de Markowitz para chegar à carteira ótima. Observa-se que o modelo B-L tende a gerar carteiras menos extremas e mais estáveis do que as de Markowitz. Certas formulações de B-L permitem ao investidor especificar o grau de confiança de suas expectativas, o que resulta em alocações mais ou menos influenciadas pela visão do investidor vis-à-vis às da carteira de mercado. Por fim, B-L permite ao investidor expressar visão de retorno relativo entre ativos, e não apenas retorno, absoluto como no modelo de Markowitz.
Exemplo prático da carteira de mercado de equilíbrio
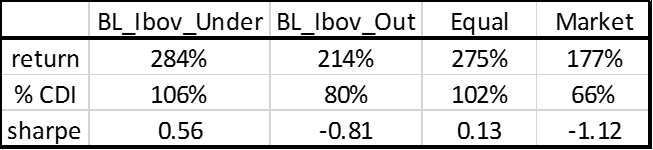
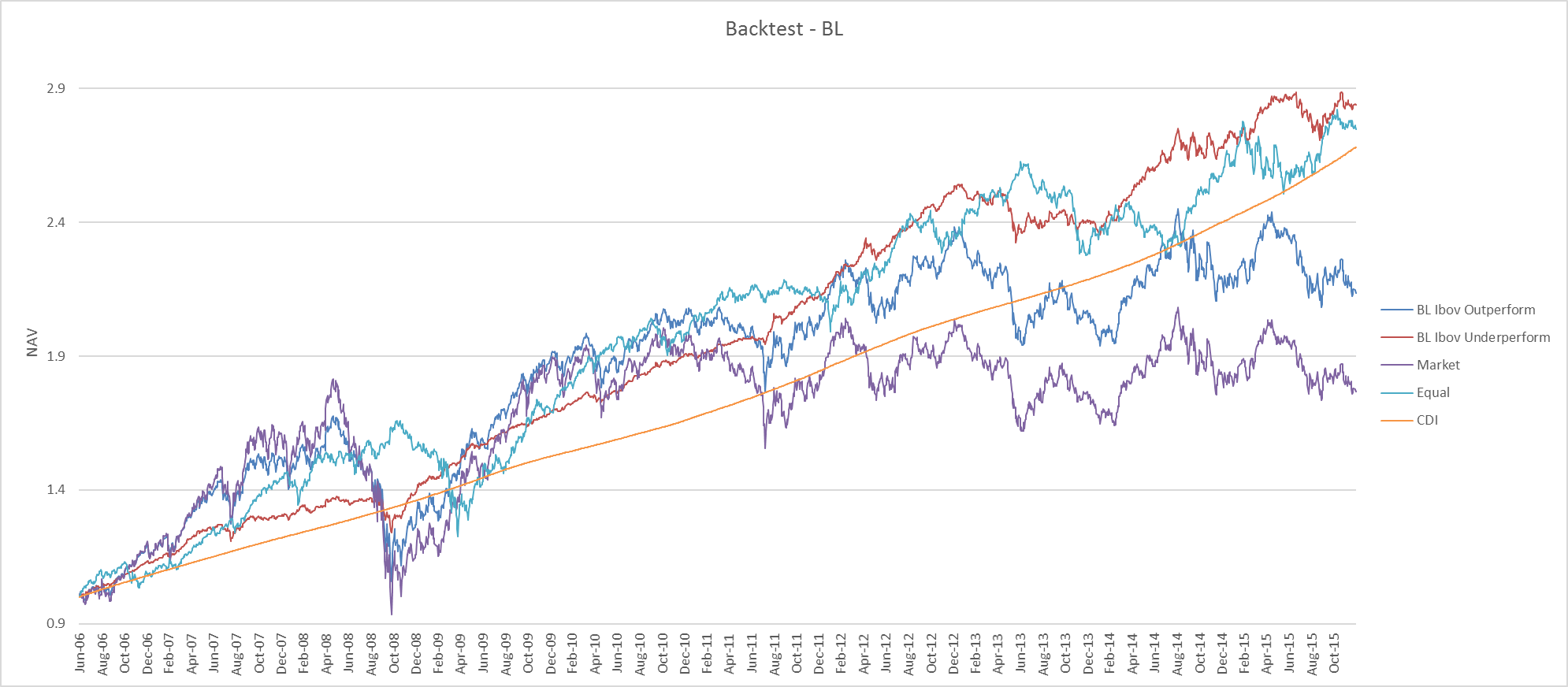
Como ilustração realizamos backtest com dados de junho 2006 a outubro de 2015 (ver gráfico 1). Simulamos quatro carteiras que alocam entre três ativos: Ibovespa, títulos de renda-fixa (IRFM) e títulos indexados a inflação (IMA-B; ver gráfico 1). Duas das carteiras foram construídas utilizando o modelo B-L: Ibov_Outperform, que expressa uma visão otimista para o mercado de ações; e Ibov_Underperform, que expressa uma visão pessimista. A título de referência, simulamos também duas carteiras passivas: a carteira de mercado (Market) e uma carteira contendo os três ativos em pesos iguais (Equal). As carteiras B-L eram recalibradas a cada período de 30 dias, com base nos dados dos 90 dias precedentes. A simulação revela que a carteira Ibov_Underperform teria obtido o maior retorno no período (o que se explica, a posteriori, pelo mau desempenho do Ibovespa), com 106% da taxa livre-de-risco (CDI). A carteira Equal teria gerado o segundo melhor retorno, mas com volatilidade significativamente maior do que Ibov_Underperform: de fato, o índice sharpe da carteira Equal é de 0,13, versus 0,56 da carteira Ibov Underperform (ver tabela 1). As carteiras Ibov Outperform e Market apresentaram retorno abaixo do CDI, sendo que esta última teve a pior performance dentre todas as carteiras.
É interessante notar que a performance da carteira Equal – que não utiliza qualquer tipo de otimização – não fica muito aquém da carteira otimizada com B-L. A pequena diferença de performance entre a carteira passiva e a carteira otimizada observada em nossa simulação é, em certa medida, típica. Ela motiva críticas a modelos de alocação em geral, e a algoritmos de alocação automática em particular: a melhora de performance obtida via modelos de alocação, se é que existe, seria pequena demais para justificar seu uso. No caso do modelo B-L a performance depende em grande parte da “visão” do investidor – isto é, de sua habilidade de corretamente antever movimentos de mercado. Ou seja, além de ciência, o modelo B-L exige uma dose de “arte” que vem da habilidade do alocador. Resta tentar modelar, de forma sistemática e replicável, essa habilidade.