Gostaríamos de parabenizar a todos que se desafiaram a solucionar o Giant Puzzle #3! Admiramos imensamente aqueles que se arriscam a pensar fora da caixa e a encontrar soluções criativas para problemas complexos.
Conseguiram resolver esse puzzle: Guilherme Sá, João Vieira, Lucas Gregolin Dias, Fabio Nassar, Lucas Sobrinho, Daniel Ramos, Guilherme Echelmeier, André Lorenzo Bittencourt, Vitor Santa Rosa, Gabriel Sarkis, Bruno Sphair, Fabio Reale, Felipe Buzato, Matheus Laranja, Hugo Ricardo Matarozzi, João Chaves, Raffaello Caser, Victor Abicalil, Felipe Moret, Luiz Castelo Branco, Alexander Costa Nunes, Paulo Ricardo Lira, João Pedro Candido, Caio Botelho Gomes, Felipe Penna, Erick Amaral Costa, Alexandre Cesar, Fabio Fernandes, Thiago Rissotto, Fabrizio Bernardi, Victor Seixas e Karina Suemi Awoki.
O problema
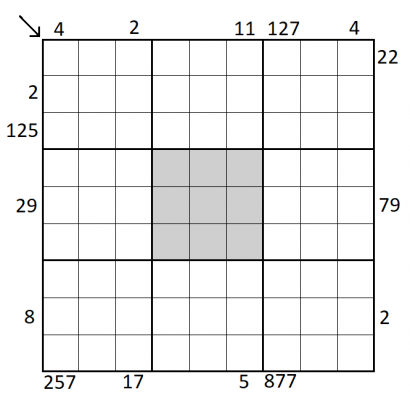
As regras normais do sudoku são aplicáveis. Além disso, o setor em destaque é um quadrado mágico* e os números externos ao grid representam os divisores dos números de 9 dígitos, quando lidos naquela direção.
Exemplo:

2 é divisor de 843791652
1091 é divisor de 256197348
Qual o maior número primo que divide o número formado pelos 9 elementos da diagonal principal do grid?
*A soma dos números das colunas, linhas e diagonais é igual
Resoluções
Foram diversas estratégias de resolução diferentes submetidas e vamos resumir aqui algumas delas, demonstrando como pensar fora da caixa e de maneira criativa aproximou cada um da resolução correta do problema.
“Comecei fazendo um programa para gerar e testar soluções candidatas. Ela preenche aleatoriamente com os números faltantes na linha/coluna e checa se as divisões são inteiras.
Então fui para o quadrado mágico, que eu achei que teria um numero mais limitado de soluções e testei a linha central, limitando à dois quadrados. Segui para coluna 127/877 e continuei testando. Eventualmente segui a lógica de um jogo de Sudoku para conseguir mais quadrados e a testar as linhas/colunas.
Até que, quase completando todo o Sudoku, cheguei num ponto em que as linhas/colunas tinham muitas soluções cada. Fui por outro caminho e vi que só tinham 3 quadrados completos possíveis, pelas regras do Sudoku. Testei cada um dos três no programa e felizmente só uma era aceitável. Depois foi só rodar uma rotina de fatoração.”
– ANDRÉ LORENZO
Resolução completa >“Escrevi um código em Python para resolver o desafio do Sudoku.
Consegui reduzir a uma única solução para a tabela: a diagonal sendo 219456894, que possui como fatores primos 2, 3, 61, 109, 5501.
Logo, a resposta procurada é: 5501.”
– LUCAS SOBRINHO
”Resolução– VITOR SANTA ROSA
Resolução completa >“Minha solução foi um híbrido de análise manual e automatizada.
Eu fiz um script em Python que em que eu listava as restrições para uma linha e obtinha as opções. Uma vez que determinava mais células, manualmente modificava o código.”
– VICTOR SEIXAS
Resolução completa >“Valeu pelo puzzle, esse foi bem divertido solucionar.
Anexei uma explicação da linha de pensamento que usei para resolver o problema.”
– GABRIEL SARKIS
Resolução completa >“Usei Python e Jupyter Notebook com as bibliotecas itertools e pandas “
– ALEXANDER NUNES
Resolução completa >“a) Com os números externos obtive as seguintes informações:
– os múltiplos de 5 terminam em 5
– os múltiplos de 125 terminam em 25 ou 75
– os múltiplos de 2, 4, 8 terminam em par (diferente de zero)
– os múltiplos de 4 terminam em 4 ou 8 dado que, nesse sudoku, o penúltimo dígito… “
– KARINA AWOKI
Resolução completa >“Resolvi então usando MiniZinc, que é uma linguagem de constraint programming. Programei os requisitos de Sudoku, divisibilidade e quadrado mágico, com isso obtive a solução do Sudoku e depois foi só fatorar a diagonal.”
– ALEXANDRE CESAR
“Bom, de início observei que 3 dos 5s eram muito evidentes: o do meio pelo quadrado mágico, os outros 2 por divisibilidade por 5 (e não existência de 0s no Sudoku). Após esse breve início, segui uma estratégia de ver quais regras de divisibilidade criavam mais restrições e ir eliminando possibilidades dessa forma.
– FABIO REALE
“Para resolver eu fiz um programa em Python para gerar todos os múltiplos de 9 dígitos dos números que estavam externos ao grid, e um outro programa para testar os números resolvendo o Sudoku. Fui filtrando os múltiplos que não serviam no problema até que encontrei uma solução final possível e estava realmente certa.”
– THIAGO RISSOTTO
– FELIPE MORET
– PAULO LIRA
– DANIEL RAMOS
– FELIPE PENNA
– GUILHERME ECHELMEIER
“Neste puzzle acabei utilizando um pouco de ‘força bruta’, onde fiz um script em Python que me voltasse com todas combinações possíveis de números entre 123456789 e 987654321 que fossem divisíveis pelos números indicados e que seus inversos fossem divisíveis ao mesmo tempo pelo número na outra ponta da tabela (Ex: Na linha central peguei todas as combinações divisíveis por 29 e que seus inversos fossem divisíveis por 79).
Depois desse primeiro ‘filtro’, comecei a entrar mais no específico de cada linha, como nesse exemplo entre (29,79), dado que ele cruzava o centro do quadrado mágico, eu teria certeza que a linha correta teria nos seus números centrais uma das possíveis combinações [‘357’, ‘753’, ‘951’,’159′].
– JOÃO CHAVES
Acesse o Giant Puzzle mais recente.

