Solução do Giant Puzzle #13 – Dovish It

Parabéns a todos que se desafiaram a solucionar o Giant Puzzle #13! Admiramos imensamente aqueles que se arriscam a pensar fora da caixa e a encontrar soluções criativas para problemas complexos.

Conseguiram resolver esse puzzle:

1. Andre Costa
2. Gustavo Aldama Mourão Soares Pereira
3. Igor Dias
4. Ivan Petrin
5. Lucas De Andrade Santos Duarte
6. Lucas Giacone
7. Victor Marques Moreno

 

Imagine que você está em um salão de um restaurante fechado. Um pássaro entra pela janela e começa a voar aleatoriamente por cima das mesas. Você quer saber qual a probabilidade de sua mesa ser “premiada”.

Vamos modelar o problema da seguinte maneira. Imagine que o restaurante tem n mesas enfileiradas em linha reta e que a janela pela qual o pássaro entrou está na mesa 1. Considere que, após o pássaro entrar, as janelas e portas estão todas fechadas.

Considere que o pássaro se move em intervalos de 1 segundo e que, no instante t, ele tem 50% de probabilidade de ficar onde está e 50% de se mover para uma mesa vizinha. Por exemplo, se ele está sobrevoando a mesa 3, ele tem 50% de probabilidade de ficar na mesa 3, 25% de ir para a mesa 4 e 25% de ir para a mesa 2. No caso de ele estar sobrevoando a mesa n ou a mesa 1, ele tem 50% de probabilidade de ficar na mesma mesa e 50% de probabilidade de ir para a única mesa vizinha.

(a) Suponha que o restaurante tem 5 mesas (n=5). Supondo que uma mesa foi “premiada” após exatamente 10 segundos, qual é a probabilidade de ter sido a mesa de número 5?
(b) Defina p(t, k) como: “supondo que uma mesa foi “premiada” após exatamente t segundos, qual a probabilidade de ter sido a mesa k.” Qual o menor valor de t tal que p(t, 5) está entre 12% e 13%?

 

Solução

Considere um vetor

P(t)P(t)

em que a entrada

kk

é

p(t,k)p(t, k)

, a probabilidade de se estar em

kk

no instante

tt

. Pode-se definir uma matriz de transição para a dinâmica do problema, em que a entrada

(i,j)(i,j)

é a probabilidade de irmos da casa

jj

para a

ii

em um passo:

A=(p1→1p2→1p3→1…pn→1p1→2p2→2p3→2…pn→2⋮p1→np2→np3→n…pn→n)A = \begin{pmatrix}
p_{1 \rightarrow 1} & p_{2 \rightarrow 1} & p_{3 \rightarrow 1} & \dots & p_{n \rightarrow 1} \\
p_{1 \rightarrow 2} & p_{2 \rightarrow 2}& p_{3 \rightarrow 2} & \dots & p_{n \rightarrow 2} \\
& & \vdots & & \\
p_{1 \rightarrow n} & p_{2 \rightarrow n} & p_{3 \rightarrow n} & \dots & p_{n \rightarrow n} &
\end{pmatrix}

De modo que podemos resolver

P(t)P(t)

recursivamente:

P(t+1)=AP(t)⟹P(t)=AtP(0)P(t+1) = A P(t) \implies P(t)=A^tP(0)

Para

n=5n=5

, temos

A=(0.50.250000.50.50.250000.250.50.250000.250.50.50000.250.5)eP(0)=(10000)A=\begin{pmatrix}
0.5 & 0.25 & 0 & 0 & 0 \\
0.5 & 0.5 & 0.25 & 0 & 0 \\
0 & 0.25 & 0.5 & 0.25 & 0 \\
0 & 0 & 0.25 & 0.5 & 0.5 \\
0 & 0 & 0 & 0.25 & 0.5 \\
\end{pmatrix} \quad \text{e} \quad P(0) =
\begin{pmatrix}
1 \\
0 \\
0 \\
0 \\
0 \\
\end{pmatrix}

Calculando em um computador, obtemos:

P(10)=(0.17660.32260.24950.17740.0739)P(10)= \begin{pmatrix}
0.1766 \\
0.3226 \\
0.2495 \\
0.1774 \\
0.0739
\end{pmatrix}

Portanto, a resposta do item a) é

7.39%7.39 \%

Para o item b), calculamos

P(t)P(t)

para

t=1,2,3,…t=1, 2, 3, …

O primeiro valor de

tt

para o qual

p(t,5)p(t, 5)

está entre

0.120.12

e

0.130.13

é

t=25t=25

.

Por que a probabilidade de acabarmos nas pontas aparenta convergir para metade da probabilidade de acabarmos no meio quando

t→∞t \rightarrow \infty

?
Para

t=25t=25

, por exemplo, o vetor de probabilidades fica

P(25)=(0.12980.25670.250.24330.1202)P(25) = \begin{pmatrix}
0.1298 \\
0.2567 \\
0.25 \\
0.2433 \\
0.1202
\end{pmatrix}

Entenderemos melhor a dinâmica do problema se nos livrarmos da assimetria nas pontas: ao invés de considerar que as mesas 1 e n só tem um vizinho, estenda o salão infinitamente de modo que todos tenham dois vizinhos:

123⋯(n−1)n1 \:\: 2 \:\: 3 \:\: \cdots (n-1) \:\: n ⇓\Downarrow ⋯32123⋯(n−1)n(n−1)⋯\:\:\:\:\:\:\:\:\: \cdots \:\: 3 \:\: 2 \:\: 1 \:\: 2 \:\: 3 \:\: \cdots (n-1) \:\: n \:\: (n-1) \:\: \cdots

Isto é, cada mesa terá infinitas “cópias virtuais”, de modo que, por exemplo, quando o pássaro vai da mesa 1 para a mesa 2 do restaurante, no salão estendido ele tem a opção de ir para a mesa 2 ou para a 2 virtual. Assim, podemos considerar que o pássaro sempre vai para esquerda, direita ou fica parado com probabilidades de 25%, 25% e 50%, respectivamente.

Mais formalmente, associamos cada mesa do restaurante a um subconjunto dos inteiros, de modo que quando o pássaro estiver sobre a mesa

kk

, o pássaro virtual estará sobre algum dos inteiros associados à mesa

kk

. O diagrama abaixo ilustra parte do salão estendido para

n=5n=5

: o eixo

yy

apresenta a mesa no salão normal e o eixo

xx

, os inteiros associados no salão estendido.

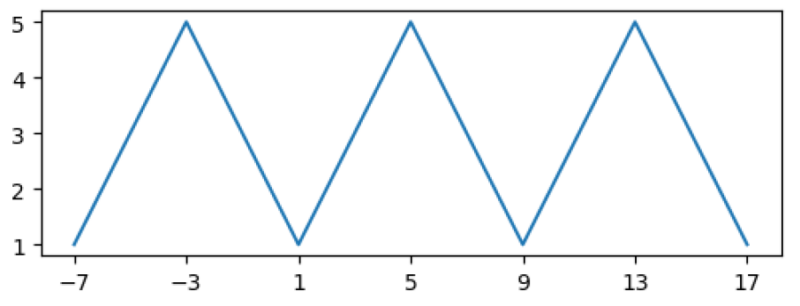
Agora fica evidente o por quê da probabilidade do pássaro estar nas pontas converge para metade da probabilidade de estar em uma mesa do meio: cada período da associação

mesa↔inteiro\text{mesa} \leftrightarrow \text{inteiro}

tem apenas 1 inteiro associado às mesas 1 e

nn

, mas dois inteiros associados às mesas do meio (visualmente, um na “subida” e outro na “descida”).

Na verdade, o salão virtual nos dá muito mais que mera intuição sobre a dinâmica do problema. Com a devida diligência, podemos calcular

p(t,k)p(t, k)

explicitamente para qualquer par

t,kt, k

.

Para tanto, vamos introduzir a função geratriz do movimento do pássaro:

Ft(x)=x1(0.5×0+0.25×1+0.25x−1)tF_t(x)=x^1(0.5x^0 + 0.25x^1 +0.25 x^{-1})^t

Essa série nos é útil pois o coeficiente do termo

xkx^k

em sua expansão é exatamente

p¯(t,k)\overline{p}(t,k)

, a probabilidade do pássaro acabar sobre a mesa virtual

kk

após

tt

segundos:

Ft(x)=∑kakxk:ak=p¯(t,k)F_t(x)=\sum_{k}{a_k x^k} \quad \text{:} \quad a_k=\overline{p}(t,k)

Portanto, para acharmos

p(t,k)p(t,k)

, basta somar os coeficientes

ak′a_k \prime

de todos os inteiros

k′k^{\prime}

associados à mesa k:

p(t,k)=∑k′assoc.kp¯(t,k′)=∑k′assoc.kak′p(t,k)=\sum_{k^{\prime} \text{assoc.} k}{\overline{p}(t,k^{\prime})}=\sum_{k^{\prime} \text{assoc.} k}{a_{k \prime }}

Vamos explorar um pouco melhor

Ft(x)F_t(x)

:

Ft(x)=x1(0.5×0+0.25×1+0.25x−1)t=x1(2x+x2+1)t22txtF_t(x)=x^1(0.5x^0 + 0.25x^1 +0.25 x^{-1})^t = x^1\frac{(2x+x^2+1)^t}{2^{2t}x^t} ⟹Ft(x)=(x+1)2t22txt−1=∑kakxk\implies F_t(x)=\frac{(x+1)^{2t}}{2^{2t}x^{t-1}}=\sum_{k}{a_k x^k}

No caso particular de

n=5n=5

e

k=5k=5

, os inteiros associados à mesa 5 são os inteiros da forma

8x+58x+5

(Verifique você mesmo!). Portanto:

p(t,5)=∑k=8x+5akxkp(t, 5)=\sum_{k=8x+5}{a_kx^k}

Mas como achamos a soma de um subconjunto dos coeficientes de uma série?
A soma do conjunto de todos os coeficientes é fácil:

∑kak=∑kak1k=Ft(1)=(1+1)2t22t1t−1=1\sum_k{a_k}=\sum_k{a_k1^k}=F_t(1)=\frac{(1+1)^{2t}}{2^{2t}1^{t-1}}=1

Para o nosso subconjunto, podemos usar uma ideia parecida: substituir valores de x em

Ft(x)F_t(x)

para ficarmos só com coeficientes, mas de forma que os coeficientes que não são da forma

8x+58x+5

“sumam”. Podemos fazer isso se olharmos para uma série ligeiramente diferente,

G(x)=x3Ft(x)G(x)=x^3F_t(x)

, e utilizarmos a oitava raiz primitiva da unidade

ζ=e2πi8=cis(2π8)\zeta=e^{\frac{2\pi i}{8}}=cis(\frac{2\pi}{8})

.

O poder de

ζ\zeta

reside no fato de que

(ζi)0+(ζi)1+…+(ζi)7=ζ8i−1ζi−1={0se 8 não divide i8se 8 divide i(\zeta^i)^0+(\zeta^i)^1+\dots+(\zeta^i)^7=\frac{\zeta^{8i}-1}{\zeta^i-1} =\begin{cases}
0 & \text{se 8 não divide i} \\
8 & \text{se 8 divide i}
\end{cases}

Logo,

G(ζ0)+G(ζ1)+…G(ζ7)8=∑k=8x+5akondeG(x)=(x+1)2t22txt−4\frac{G(\zeta^0)+G(\zeta^1)+\dots G(\zeta^7)}{8}=\sum_{k=8x+5}{a_k} \quad \text{onde} \quad G(x)=\frac{(x+1)^{2t}}{2^{2t}x^{t-4}}

pois os únicos termos de

GG

que “sobrevivem” são aqueles que multiplicam potências de x múltiplas de 8, isto é, exatemente os

a8x+5a_{8x+5}

. Vamos às contas:

G(ζ0)=G(1)=(1+1)2t22t1t−4=1G(\zeta^0)=G(1)=\frac{(1+1)^{2t}}{2^{2t}1^{t-4}}=1 G(ζ4)=G(−1)=(1−1)2t22t(−1)t−4=0G(\zeta^4)=G(-1)=\frac{(1-1)^{2t}}{2^{2t}(-1)^{t-4}}=0 G(ζ2)=G(i)=(i+1)2t22tit−4=2tcis(π42t)22tit−4=t=25cis(π2)225i1=1225G(\zeta^2)=G(i)=\frac{(i+1)^{2t}}{2^{2t}i^{t-4}}=\frac{2^tcis(\frac{\pi}{4}2t)}{2^{2t}i^{t-4}} \overset{t=25}{=}\frac{cis(\frac{\pi}{2})}{2^{25}i^1}=\frac{1}{2^{25}} De maneira similar,G(ζ6)=1225\text{De maneira similar,} \quad G(\zeta^6)=\frac{1}{2^{25}}

Para

G(ζ)G(\zeta)

, foquemos no numerador

(ζ+1)2t(\zeta+1)^{2t}

:

(ζ+1)=(cis(2π/8)+1)=((22+1)+22i)=(\zeta+1)=(cis(2\pi/8)+1)=((\frac{\sqrt{2}}{2}+1)+\frac{\sqrt{2}}{2} i)= 2+2(2+22+2−22i)=2+2cis(π8)\sqrt{2+\sqrt{2}}(\frac{\sqrt{2+\sqrt{2}}}{2}+\frac{\sqrt{2-\sqrt{2}}}{2} i)=\sqrt{2+\sqrt{2}} \:\: cis(\frac{\pi}{8}) ⟹(ζ+1)2t=(2+2)tcis(π82t)\implies (\zeta+1)^{2t}=(2+\sqrt{2})^t \:\: cis(\frac{\pi}{8}2t) G(ζ1)=(ζ+1)2t22tζt−4=(2+2)t22tcis(π82t)cis(2π8(t−4))=t=25−(2+2)25425G(\zeta^1)=\frac{(\zeta+1)^{2t}}{2^{2t}\zeta^{t-4}}=\frac{(2+\sqrt{2})^t}{2^{2t}}\frac{cis(\frac{\pi}{8}2t)}{cis(\frac{2\pi}{8}(t-4))} \overset{t=25}{=} -\frac{(2+\sqrt{2})^{25}}{4^{25}} De maneira similar,G(ζ7)=−(2+2)25425eG(ζ3)=G(ζ5)=−(2−2)25425\text{De maneira similar,} \quad G(\zeta^7)= -\frac{(2+\sqrt{2})^{25}}{4^{25}} \quad \text{e} \quad G(\zeta^3)=G(\zeta^5)= -\frac{(2-\sqrt{2})^{25}}{4^{25}}

Portanto,

∑k=8x+5ak=G(ζ0)+G(ζ1)+…G(ζ7)8=1+0+2(1225−(2+2)25425−(2−2)25425)8\sum_{k=8x+5}{a_k} = \frac{G(\zeta^0)+G(\zeta^1)+\dots G(\zeta^7)}{8} = \frac{1+0+2(\frac{1}{2^{25}}-\frac{(2+\sqrt{2})^{25}}{4^{25}}-\frac{(2-\sqrt{2})^{25}}{4^{25}})}{8} ⟹p(25,5)=18−14(2+2)25+(2−2)25−225425=0.12022793196…\implies p(25, 5)=\frac{1}{8}-\frac{1}{4} \frac{(2+\sqrt{2})^{25}+(2-\sqrt{2})^{25}-2^{25}}{4^{25}} = 0.12022793196…

A fórmula geral para qualquer

tt

da forma

8x+18x+1

fica

p(t,5)=18−14(2+2)t+(2−2)t−2t4tp(t, 5)=\frac{1}{8}-\frac{1}{4} \frac{(2+\sqrt{2})^{t}+(2-\sqrt{2})^{t}-2^{t}}{4^{t}}

 

Resolução: Olavo Longo – Giant Steps