Parabéns a todos que se desafiaram a solucionar o Giant Puzzle #2! Recebemos mais de 150 respostas ao longo dos 2 meses que o desafio ficou no ar. Solucionaram esse puzzle:
Itens a, b e c: Lucas Sobrinho, Henrique Leone Alexandre, Daniel Ramos Bezerra de Alencar, Ana Paula Schuch, Juliano Negri, Matheus Laranja, Raphael Sisson, Lucas Gregolin Dias, Gabriel Sarkis, Felipe Moret, Victor Seixas Souza, Guilherme Echelmeier, Guilherme Sá, Felipe Buzato, Daniel Daher, Maurício Andrade e João Vitor Vieira;
Itens a e b: Leonardo Joau, Mauricio Bandeira, Felipe Teixeira Silva, Roberto Garcia, André Lorenzo Bittencourt, Rogerio Chaves, Danilo Fernandes e Nicolas Perez.
Solução – Giant Puzzle #2
Pedro deseja encher 3 canecas de 500 mL de uma mesa com chopp usando um balde de 5L. Para fazer isso, ele enche o balde com 5L de chopp em um barril e leva até a mesa, enchendo as canecas. Porém, Pedro está bêbado e, sempre que volta do barril até sua mesa, perde uma quantidade aleatória de chopp com distribuição uniforme sobre a capacidade do balde. Ele, então, preenche as canecas com o que houver de chopp no balde (pode preencher mais de uma caneca com o chopp do balde). Por isso, pode ser necessário que Pedro faça mais de uma viagem até ter todas as canecas cheias.
A) Qual a probabilidade de Pedro encher as canecas em sua N-ésima viagem?
A soma de N variáveis uniformes possui a distribuição de Irwin-Hall, de forma que a função densidade de probabilidade vale x^(n-1)/(n-1)! se 0 ≤ x ≤ 1. Assim, a probabilidade de encher M canecas em N viagens, com M ≤ 10, vale:
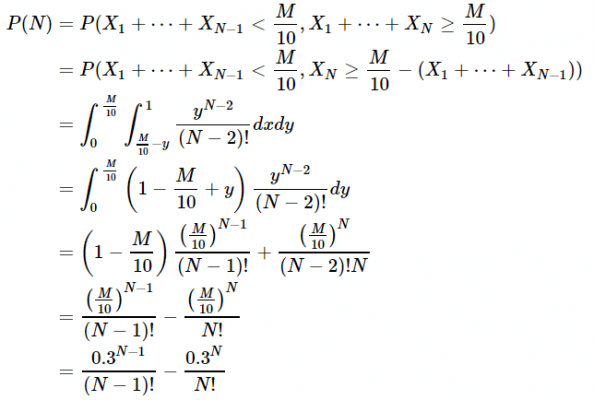
B) Em média, quantas viagens Pedro deve fazer para encher as 3 canecas?
Usando a resposta do item anterior e a expansão em série de Taylor da função exponencial, temos que o valor esperado para encher 3 canecas vale:
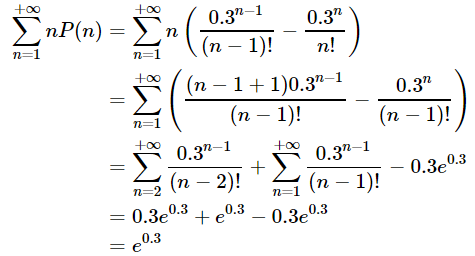
C) Quantas viagens Pedro deveria fazer, em média, para encher N canecas de chopp, sendo N um número natural qualquer?
De forma geral, para N ≤ 10, a resposta do item anterior vale e^(N/10). Já para o caso N > 10, chamando N/10 = x e o valor esperado de viagens pedido de f(x) podemos construir a seguinte equação de recorrência:
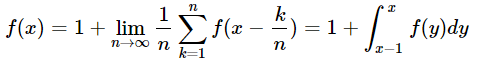
Derivando a expressão acima e substituindo o valor f(x-1) = e^(x-1) para 1 ≤ x ≤ 2, temos:
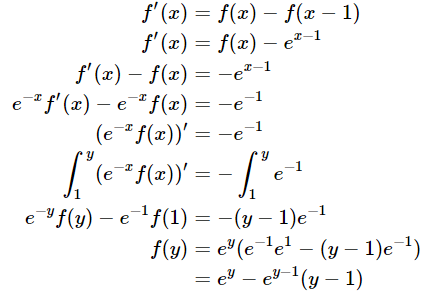
A resposta acima é válida para 1 ≤ y ≤ 2, pois é este o intervalo no qual o valor substituído para f(x-1) é válido. De forma geral, temos:
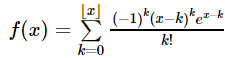
Este resultado pode ser provado por indução utilizando-se a expressão acima de forma análoga ao resultado anterior. Vale ressaltar que o resultado do item b também pode ser encontrado utilizando-se uma expressão de recorrência semelhante à exibida acima.
Se você quer aprender mais sobre matemática e estatística, publicamos aqui no nosso site a Biblioteca Giant, com todas as referências mais importantes que usamos no desenvolvimento das nossas estratégias de investimento.
Clique aqui para acessar o nosso mais novo puzzle! Esperamos pela sua resposta.

