Parabéns a todos que se desafiaram a solucionar o Giant Puzzle #4! Admiramos imensamente aqueles que se arriscam a pensar fora da caixa e a encontrar soluções criativas para problemas complexos.
Conseguiram resolver esse puzzle: Leonardo Joau, Saul Spatz e Guillermo Wildschut.
O problema
Rodrigo é um colecionador de figurinhas e deseja completar um álbum de futebol que foi lançado. Considere que o álbum possui 680 figurinhas a serem coladas, das quais 80 são holográficas. As figurinhas holográficas são 5 vezes mais raras que as normais, ou seja, a probabilidade de uma delas aparecer em um pacote de figurinha é 1/5 vezes a probabilidade de aparecer uma não-holográfica. Considere que os pacotes contêm 7 figurinhas cada e elas podem aparecer repetidas dentro de um mesmo pacote. Ainda, cada um dos pacotes custa 40 centavos em uma banca de jornal.
a) Calcule o valor esperado gasto por Rodrigo (em reais) para completar o álbum, considerando que ele não faça trocas.
b) Suponha que exista um mercado paralelo de venda de figurinhas individuais, as quais Rodrigo pode escolher separadamente para completar o álbum. Cada figurinha normal custa 30 centavos, enquanto uma holográfica custa 2 reais. Considere que Rodrigo compra pacotes de figurinhas até um ponto em que vale a pena ele comprar todas as restantes individualmente. Calcule o valor esperado gasto por Rodrigo neste caso.
c) Resolva os mesmos problemas dos itens a e b, porém considerando que não podem vir figurinhas repetidas num mesmo pacote.
Observação: expresse suas respostas com 8 casas decimais de precisão.
Solução
a) 874.09642499
b) 199.60637310
c) 869.91971711 e 199.19343404
A melhor forma para chegar nestes valores consistia em resolver um problema de programação dinâmica.
Considere f(n,k) o número esperado de pacotes a serem comprados quando faltam n figurinhas normais e k holográficas.
Considere também p_{i,j;k,l} a probabilidade de uma pessoa que tem um álbum faltando i figurinhas normais e k holográficas que, ao comprar um pacotinho, tem um saldo de figurinhas faltantes de j normais e l holográficas.
Esse valor esperado obedece à seguinte recursão:
![]()
A equação acima pode ser rearranjada da seguinte forma:
![]()
Assim que faltarem n figurinhas normais e k holográficas para um determinado colecionador, ele deve checar se vale a pena comprar todas as figurinhas restantes no mercado paralelo ou se deve apostar em comprar mais um pacotinho.
Por isso, o valor resultante da recursão acima deve ser armazenado em uma matriz como sendo o menor entre i) a esperança de conseguir as figurinhas faltantes comprando um pacotinho ou ii) comprar tudo no mercado paralelo.
Ainda, dado que a figurinha holográfica é 5 vezes mais rara que a normal, a probabilidade de uma figurinha aleatória ser normal é:
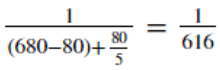
O código em anexo mostra a solução genérica comentada para os itens a e b. O que muda para o item c é a probabilidade de obter uma figurinha repetida normal ou holográfica dentro de um pacotinho, já que deve ser considerada a influência das figurinhas anteriores que já foram retiradas dentro dele. O código em anexo também ilustra como esse problema pode ser resolvido.
A solução está disponível através do link abaixo.
https://github.com/giant-steps/giant-puzzle-4

